¿Qué es una REGRESIÓN LINEAL SIMPLE? Con ejemplos

Las regresiones son de las herramientas más usadas en estadísticas, te sirve para obtener ecuaciones que describen la relación entre dos o más variables de las cuales conocemos un conjunto de datos. En este artículo verás la regresión lineal simple y entenderás en qué casos usarla, cómo usarla y cuándo no deberías usarla.

Contenido

¿Qué es una regresión lineal simple?
¿Para qué sirven las regresiones lineales?
Aplicaciones de las regresiones lineales
Descripción técnica del problema de regresión lineal simple
Cómo hacer una regresión lineal
1. En Python
2. En excel
Ejemplo de una regresión lineal
¿Dónde no debes aplicar las regresiones lineales simples?

¿Qué quiere decir y qué es una regresión lineal simple?

Regresión lineal simple en análisis estadístico

La regresión lineal se refiere a un proceso en el cual inferimos un modelo matemático lineal (ecuación de una recta o un plano) basado en un conjunto de datos medidos que muestran información de la relación de varias variables cuantitativas. Específicamente la regresión lineal simple se refiere a la estimación de la ecuación de una recta, donde sólo hay una variable independiente y una dependiente.

En la imagen de la derecha puedes ver a qué se refiere con esa estimación. La recta va a relacionar un valor del eje X con otro del eje Y, la idea es que tenga la menor diferencia posible con los datos obtenidos en mediciones, que son los puntos azules.

¿Para qué sirve la regresión lineal?

La aplicación es básicamente una estimación y por lo tanto las aplicaciones pueden ser muchas. Una de ellas es estimar una variable para no medirla, una vez que encuentras la relación entre varias variables sólo necesitas conocer unas de ellas y de ahí inferir el valor de otras. Se utiliza mucho cuando medir alguna de las variables es difícil, costoso o tedioso, pero la otra o las demás no, por lo tanto esa estimación te ahorrara los costos o tiempo de realizar esa medición. Esto se conoce como sensores virtuales.

Otro caso común en el que se usa es para encontrar una tendencia de forma objetiva. Incluso se usa como regla que aporta información objetiva a la hora de tomar decisiones, con esto incluso los computadores pueden tomar dichas decisiones. Ya que es muy claro que, si la pendiente de la recta estimada es positiva, entonces la tendencia es a aumentar, pero en caso de tener pendiente negativa, entonces ocurrirá lo contrario, como se puede ver en la siguiente imagen. Lo he visto aplicar en el sector empresarial para determinar si el rendimiento de las empresas tiene tendencia creciente o decreciente.

Aplicaciones de las regresiones lineales simples

Las aplicaciones son muy variadas y realmente el límite es la imaginación de quien las quiera aplicar, aunque hay ciertas limitaciones técnicas de las que hablaré al final de este artículo, no deja de ser una herramienta muy versátil aplicable a muchísimos campos. Veamos unos ejemplos:

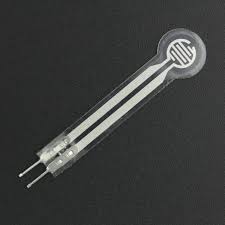
Medición de sensibilidad de un sensor de presión

Los sensores de presión son transformadores de energía mecánica en energía eléctrica. Consisten en que el voltaje de salida del sensor se modifica a diferentes presiones, pero se desconoce realmente el valor de fuerza que corresponde al voltaje, por eso se suelen hacer medidas en laboratorio, donde se le aplica una fuerza conocida y se mide el voltaje. En consecuencia, se hace la regresión lineal para que siempre se pueda estimar la fuerza o presión sobre el sensor únicamente midiendo el voltaje.

Regresión lineal aplicada a estimar la sensibilidad de un sensor

Regresión lineal aplicada a estimar el empleo de un país

Estimador de tendencia de empleo

En Perú realizaron un estudio para determinar cómo varía el empleo en el tiempo. Esto es particularmente útil cuando se quiere hacer alguna política pública de empleo o algo similar. Lo que plantea es que la tendencia en los años anteriores se mantiene, por lo que, si quiero predecir un valor de personas que encontrarán empleo en el próximo año, entonces sólo debo aplicar la ecuación de la recta obtenida con una regresión lineal basada en los datos de los años previos. Te dejo el estudio para que lo conozcas más en detalle aquí.

Estimador de tendencias de mercado

En las empresas también se necesita estimar tendencias, ya sea de sus propias utilidades, recursos, demanda de clientes o indicadores de la competencia. Así, un gerente puede determinar si las medidas tomadas en el pasado son las correctas a futuro. Una estimación a corto plazo se hace muy fácilmente usando las regresiones lineales, su implementación además es muy sencilla, lo que lo hace entendible para personas que técnicamente no tienen entrenamiento, por lo que fácilmente convence a inversionistas o accionistas de las empresas.

Aplicación de regresión lineal a mercados financieros

Descripción técnica del problema de la regresión lineal

Partimos de un conjunto de datos que muestran dos variables que se obtienen mediante una medición.

(1) $\begin{eqnarray*} x=[x_1,x_2,x_3,\cdots,x_N]^T \\ y=[y_1,y_2,y_3,\cdots,y_N]^T \\ \end{eqnarray*}$

Donde $x_i$ con $i=1,\cdots,N$ son las muestras obtenidas para la variable independiente y $y_i$ con $i=1,\cdots,N$ son las muestras obtenidas para la variable dependiente.

El objetivo es encontrar una ecuación de una recta tal que describa lo mejor posible la relación entre las variables que evidencian los datos. Esa ecuación para el caso de regresión lineal simple es una recta y matemáticamente se escribe de la siguiente manera:

(2) $\begin{equation*} \hat{y}=ax+b \end{equation*}$

Por notación vamos a aclarar que $\hat{y}$ es una estimación de $y$ , por lo tanto, son variables diferentes. No pasa lo mismo con $x$ porque es la variable independiente y se asume siempre conocida, no se estima. También en este modelo podemos observar que tenemos dos variables desconocidas que son $a$ y $b$ , dependiendo de su valor podría ser cualquier recta en un plano. Para hallarlas se plantea el siguiente problema de optimización:

(3) $\begin{eqnarray*} \min_{a,b} ee^T \\ e=y-\hat{y} \end{eqnarray*}$

La anterior expresión matemática indica que de todos los valores posibles de $a$ y $b$ vamos a tomar los que hagan que $e$ sea lo menor posible. Esa es la definición de la mejor ecuación lineal posible. La solución la describo más adelante puedes ir dando click aquí.

Sé que suena un poco complejo y si no estás relacionado con la matemática puede sonar un poco raro, pero no te preocupes, que con un ejemplo se aclara todo. Hay una sección de un ejemplo o también puedes ver el video sobre cómo hacerla en excel.

¿Cómo se realiza una regresión lineal?

Para realizarla debes seguir dos pasos, por un lado es la demostración teórica, que nos indica el procedimiento matemático. El otro paso es la implementación en un computador, porque a mano es muy difícil, en especial si tenemos muchísimos datos. Acá te dejo los pasos.

Concepto teórico de la regresión lineal

La estimación en este caso es el proceso de optimización que disminuye el error entre el valor estimado con la ecuación de la recta y el medido en la realidad, como se mostró en la sección de descripción técnica. Para encontrar la solución se debe derivar e igualar a cero la función de costo y de ahí despejar los valores de $a$ y $b$ , recuerdo que en este proceso x y y son vectores que contienen los datos medidos.

(4) $\begin{eqnarray*} d[ee^T]&=&0 \\ d[(y-[a,b][x,1_N])(y-[a,b][x,1_N])^T]&=&0 \\ \left[x,1_N\right] y^T - [a,b] [x,1_N] [x,1_N]^T &=& 0 \\ \left[a,b\right]&=& \left( [x,1_N] [x,1_N]^T\right) ^{-1} \left[x,1_N\right] y^T \end{eqnarray*}$

Donde $1_N$ es un vector de unos del tamaño de $x$ , con esto [x, 1_N] es una matriz con los dos vectores concatenados. Con esta operación de la última ecuación, ya se tiene los valores de la recta que nos dan una estimación para cualquier valor de $y$ sin necesidad de medir esta variable, sólo teniendo a $x$ .

¿Cómo aplicar el algoritmo de regresiones lineales?

Una vez demostrado el resultado sólo debemos obtener los valores de $a$ y $b$ en la ecuación anterior. De ahí podemos inferir que sólo requerimos unas multiplicaciones matriciales y la inversa de una matriz una vez los datos estén acomodados en una matriz como corresponde. Y aunque existen otras formas de realizar la regresión lineal dentro de Python, voy a indicar sólo un algoritmo, que además es fácilmente extrapolable en cualquier lenguaje de programación. Y para que sea más sencillo, lo voy a explicar por partes.

Hago la aclaración de que asumo que sabes programar y tienes conceptos básicos sobre Python. Si no los tienes, entonces esta sección te parecerá inentendible y te recomiendo mirar cómo hacerlo en Excel, que es la siguiente sección.

Comienza agregando las librerías necesarias:

####################### Librerías necesarias
import numpy as np #Librería para operaciones matemáticas
import matplotlib.pyplot as plt  #Librería para graficar

Luego creamos la función que nos hace la regresión lineal. La cual consiste en apilar los datos de las variables $x$ y $y$ de tal forma que obtengamos los valores de $a$ y $b$ , los cuales serán los resultados de la función.

################### Creación de la función que hacer la regresión lineal
def regresionMinimosCuadrados(x,y):
    x=np.array([x])
    tamanoX=np.asarray(x.shape)
    matOnes=np.ones((1,tamanoX[1]))
    xConUnos=np.concatenate((x,matOnes))
    laInv=np.linalg.inv(np.matmul(xConUnos,np.transpose(xConUnos)))
    a=np.matmul(np.matmul(laInv,xConUnos),np.transpose(y))
    return(a[0],a[1])

Luego deberías agregar los datos que vas a usar en la regresión lineal, como no tengo, entonces simplemente voy a crear unos.

################### Creación de unos datos aleatorios
numData=50
x=np.random.rand(numData)*5 #Posiciones en el eje x
ruido=2.5*(np.random.rand(numData)-0.5)   # Simulación de ruido de medición
y=2*x+1+ruido #posiciones en el eje Y

Ahora usamos la función creada para obtener la solución a nuestra regresión lineal. Además, con la función print() mostramos la solución.

################### Aplicación de la función creada
a,b=regresionMinimosCuadrados(x,y)
################### Mostrar los resultados
print('La pendiente es ')
print(a)
print('La ordenada al origen es ')
print(b)

El siguiente paso es opcional, ya que tenemos la solución, pero nunca está de más aprender a graficar nuestros datos por si debemos enseñarlos a alguien. Lo primero es obtener datos de la recta y nos aseguramos de que tenga los valores para representar todo el rango para que sea visible con los datos y luego graficamos normalmente, como lo muestro a continuación:

################### Datos para graficar
#Limites a simular
infLim=np.min(x) ##Limite inferior
supLim=np.max(x) ##Limite superior
xest=np.linspace(infLim, supLim, num=2, endpoint=True)#Puntos en el eje X de la recta
yest=a*xest+b    ##Esta es la simulación usando el estimador
################### Gráfica

plt.plot(x,y,'k.')#Grafica de los puntos de medición
plt.plot(xest,yest,'r')#Gráfica de la recta estimada 
plt.legend(['Medición','Estimación']) 
plt.xlabel('x')
plt.ylabel('y')
plt.show()

El resultado es el siguiente:

La pendiente es 
2.0444982361255404
La ordenada al origen es 
0.6873546527842443

Y la gráfica que te muestra será:

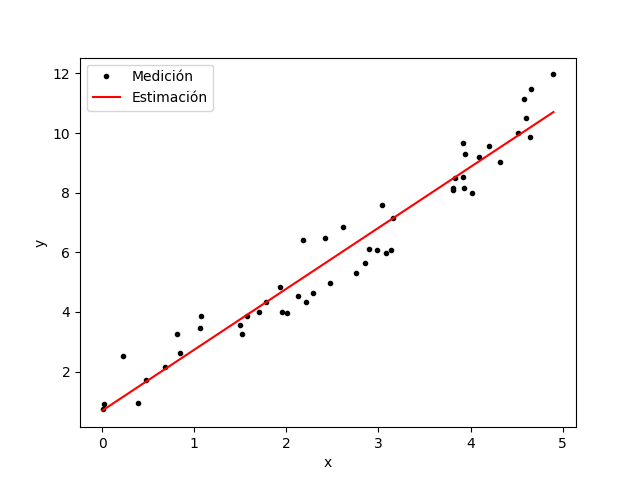
Otra forma de hacer lo mismo en Python es usando la librería scikit-learn. Te dejo el siguiente video para que puedas hacerlo de esta otra forma. Personalmente esta librería no me parece tan interesante cuando se trata de la regresión lineal, pero hay muchos procedimientos de otro tipo de regresiones y estimaciones más complejas que se pueden hacer con un procedimiento casi idéntico, por lo que sí recomiendo aprender este método.

Regresión lineal en Excel

Si no quieres usar un lenguaje de programación, lo más fácil es usar Excel. Acá te dejo un video sobre cómo hacerlo en ese tipo de hojas de cálculo.

Ejemplo de una aplicación real de una regresión lineal simple

Para que puedas entender mejor de cómo usar la regresión en la vida real, vamos a poner un ejemplo de unos datos que tiene públicos el profesor Leonel Paredes Madrid en IEEE Xplore para medir la fuerza usando sensores de presión, también puedes ver que en varios de sus artículos también ha realizado este procedimiento. El problema de las mediciones de sensores siempre es complejo y requiere de una estimación. Sabemos que usan materiales que cuando tienen presión modifican sus propiedades eléctricas, así podemos medir el voltaje y cuando sea modificado se entiende que es debido a la presión sobre el sensor, lo que nos falta averiguar es ¿qué variación de voltaje corresponde a qué tanta fuerza?

Entremos un poco más en el detalle del problema, ¿si mide 2V está relacionado con 10N o 20N de fuerza? Para conocerlo lo que se hace es aplicar al sensor fuerzas conocidas, colocando masas con peso conocido sobre el sensor. Con los cuales tendremos un vector con los valores de la fuerza y otro con los valores del voltaje medido, lo que serán nuestros datos usados en la regresión y el resultado es una ecuación que estimará la fuerza para cualquier voltaje medido.

Se tomaron las siguientes muestras y tienen los siguientes valores:

x=np.array([1.14521,1.20605,1.33675,1.49284,1.6709,1.85082,2.05852,2.28724,2.51416,2.72738,2.85677,3.03811,3.16894,3.27035,3.37025,3.51893,3.64364,3.72939,3.84799,3.9111,4.00482,1.13439,1.13796])
y=np.array([0.08143,0.1635,0.26315,0.36845,0.46556,0.57767,0.67665,0.76571,0.87273,0.9749,1.07201,1.17091,1.27327,1.38111,1.47609,1.57078,1.67569,1.78108,1.86631,1.97268,2.07487,0.07968,0.08446])

Siguiendo el procedimiento descrito en la sección del algoritmo de regresiones lineales se llega a los valores de la pendiente y de la ordenada al origen, 0.6387 y -0.6498 respectivamente. Con ellos se puede graficar la recta que indica y con los puntos de medición podemos ver que sí siguen valores similares.

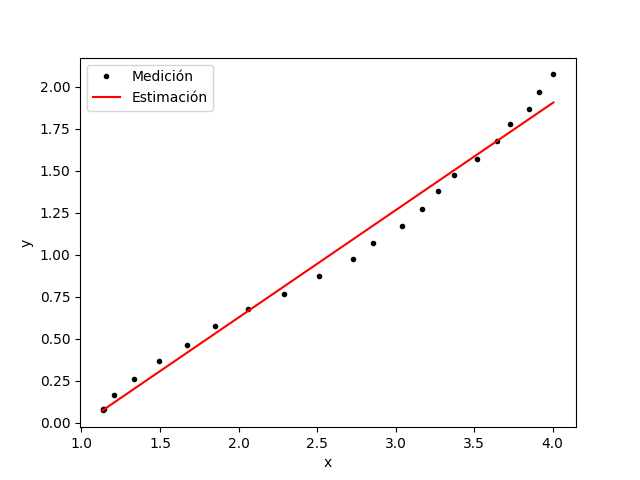
Ejemplo de una regresión lineal simple en python

La solución a nuestro problema es esta recta que cada vez que tenemos un voltaje y queremos saber la fuerza exacta, entonces sólo debemos aplicar fórmula con los valores hallados y no es necesario conocer el peso ni ningún otro valor adicional.

¿Cuándo no se aplica la regresión lineal?

Es importante que no sólo se tenga en cuenta que se pueda acceder a los costos de la misma, también se debe tener en cuenta que la información aportada por los datos no dice si es correcto o no usarla. Por eso voy a mostrar unos casos en los que se recomienda usar o no usar la regresión lineal.

No existe correlación entre los datos

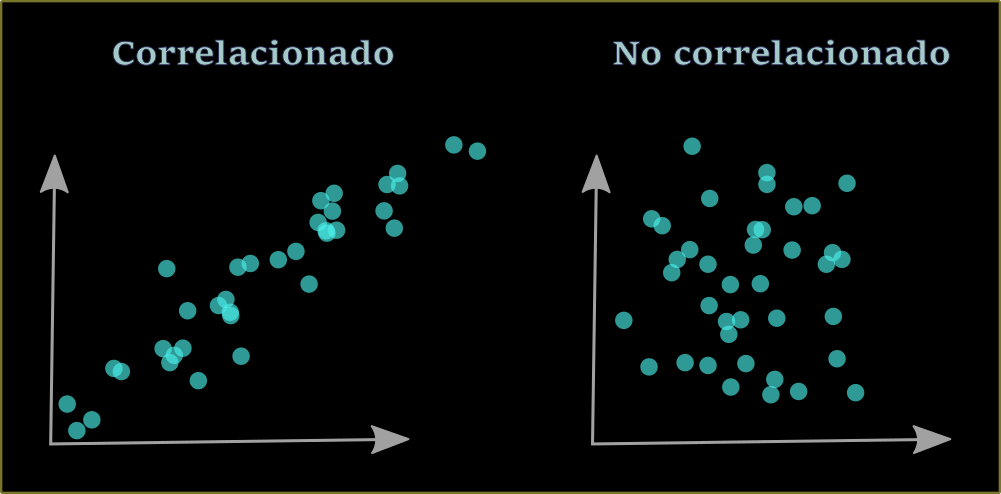
Puede ocurrir que no exista correlación entre los datos. El concepto es que, si observas que la variable dependiente cambia al modificar el valor de la variable independiente, entonces está correlacionado. En caso de que no, entonces no hay ningún modelo matemático que te ayude a describir la relación entre las variables porque sencillamente no existe. Usualmente las figuras de variables correlacionadas son delgadas, mientras que las no correlacionadas son cuadros, círculos, óvalos y figuras que son anchas. Lo puedes observar fácilmente con una gráfica, como lo muestran claramente las siguientes gráficas o comprobar usando el coeficiente de correlación lineal, que es una cuantificación numérica de la relación entre la similitud de los valores de ambas.

Regresion lineal datos no correlacionados

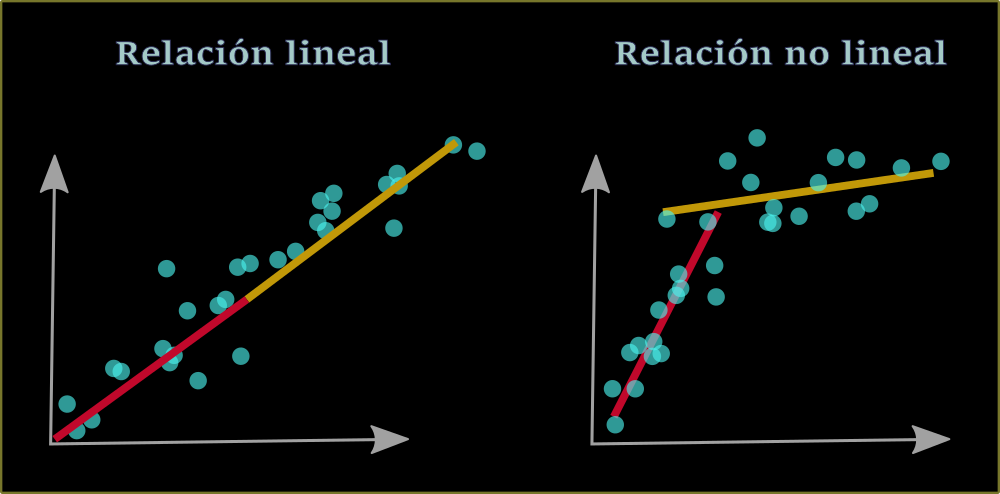
La relación no es lineal

Otro de los problemas que puedes tener es que la relación entre las variables no es lineal. O sea, aunque exista una correlación entre los datos, el modelo nunca va a representar los datos de forma precisa. Una forma fácil de verificarlo es tomar los datos de dos intervalos de la variable $x$ y hallar los valores de $a$ y $b$ de forma independiente. Si los dos varían mucho, lo más probable es que requeriremos un tipo de estimación no lineal. También puedes tomar el modelo lineal a trozos, que consiste en hallar una regresión lineal para distintos intervalos, como lo puedes ver en la siguiente imagen.

Regresión lineal a trozos para simplificar un problema no lineal

Error de estimación muy grande

Otra de las limitaciones que debes tener en cuenta a la hora de evaluar si no debes usar un modelo de regresión lineal es la magnitud aceptable de error. Cada problema tiene un margen de error aceptable, según la aplicación que le estés dando que lo puedes obtener de las consecuencias de tener un modelo con mala precisión.

Por ejemplo, es común escuchar de forma informal, usualmente en universidades, que el 10% de error es aceptable, pero en medicina, un error del 10% en la temperatura de un paciente implica pasar de 37°C a 40°C, que es pasar de una temperatura normal a una fiebre peligrosa para la salud de un paciente. En este caso sería casi impensable aceptar un error mayor a 1°C, que es menos del 3%. Por otro lado, a veces los modelos sólo buscan decir la tendencia, por lo que un error de incluso el 20% puede igualmente darnos la tendencia de forma aproximada y ser válidos. Y acá es donde nadie te puede decir qué valor es aceptable o no, debes preguntarte: ¿qué pasa si me equivoco un poco o mucho al usarla?

La forma más sencilla de visualizar el error es por medio de una gráfica, aunque también lo puedes cuantificar usando la varianza o el error cuadrático medio. Todo esto te da una idea de si el modelo tendrá un comportamiento válido o no al aplicarlo, si se determina que el error es tan grande que puede poner en riesgo la solución al problema en que quieres aplicar la regresión, entonces no lo uses.

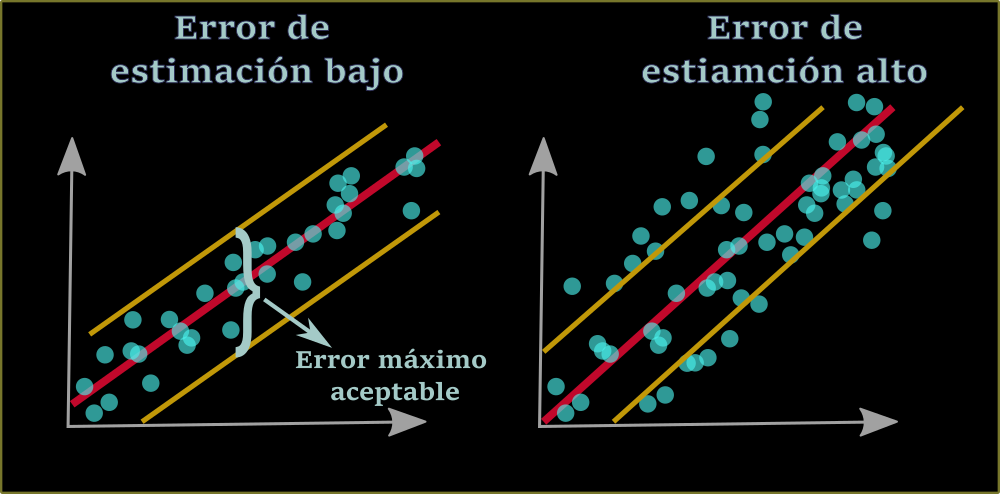
Error de estimación de una regresión lineal

En caso de que el error sea muy grande, busca alternativas como agregar más variables dependientes o una estimación no lineal.

Espero que con todo esto ya puedas aplicar la regresión lineal en los problemas que consideres que pueden ser usados.

¿Qué es la regresión lineal simple en estadística?

Contenido

¿Qué quiere decir y qué es una regresión lineal simple?

¿Para qué sirve la regresión lineal?

Aplicaciones de las regresiones lineales simples

Medición de sensibilidad de un sensor de presión

Estimador de tendencia de empleo

Estimador de tendencias de mercado

Descripción técnica del problema de la regresión lineal

¿Cómo se realiza una regresión lineal?

Concepto teórico de la regresión lineal

¿Cómo aplicar el algoritmo de regresiones lineales?

Regresión lineal en Excel

Ejemplo de una aplicación real de una regresión lineal simple

¿Cuándo no se aplica la regresión lineal?

No existe correlación entre los datos

La relación no es lineal

Error de estimación muy grande

Deja una respuesta Cancelar la respuesta